A boxplot (also known as a box and whisker plot) is a way of graphically illustrating the distribution of numeric data using the “five number summary” of the data set – namely the minimum, first quartile, median, third quartile, and maximum values. It also identifies any outliers that may exist in the data set. This tutorial will show you the easiest way to create a boxplot for a single variable in SPSS.
Quick Steps
- Click Graphs -> Boxplots in SPSS version 29
Click Graphs -> Legacy Dialogs -> Boxplots in earlier versions of SPSS - Select Simple and Summaries of separate variables
- Click Define
- Click Reset (recommended)
- Select the variable for which you wish to create a boxplot, and move it into the Boxes Represent box
- Click OK
The Data
The starting assumption for this tutorial is that you have already imported your data into SPSS, and that you’re looking at something like the data set below. (Check out our tutorials on importing data from Excel or MySQL into SPSS).
Our fictitious data set contains the Statistics final exam scores for 60 students (first 21 records displayed). We will generate a boxplot so that we can visualize the way in which these exam scores are distributed and determine whether they include any outliers.
Creating a Boxplot
The easiest way to create a boxplot is to click Graphs -> Boxplot as illustrated below. (Note that if you are using SPSS version 28 or earlier, you will need to click Graphs -> Legacy Dialogs -> Boxplot).
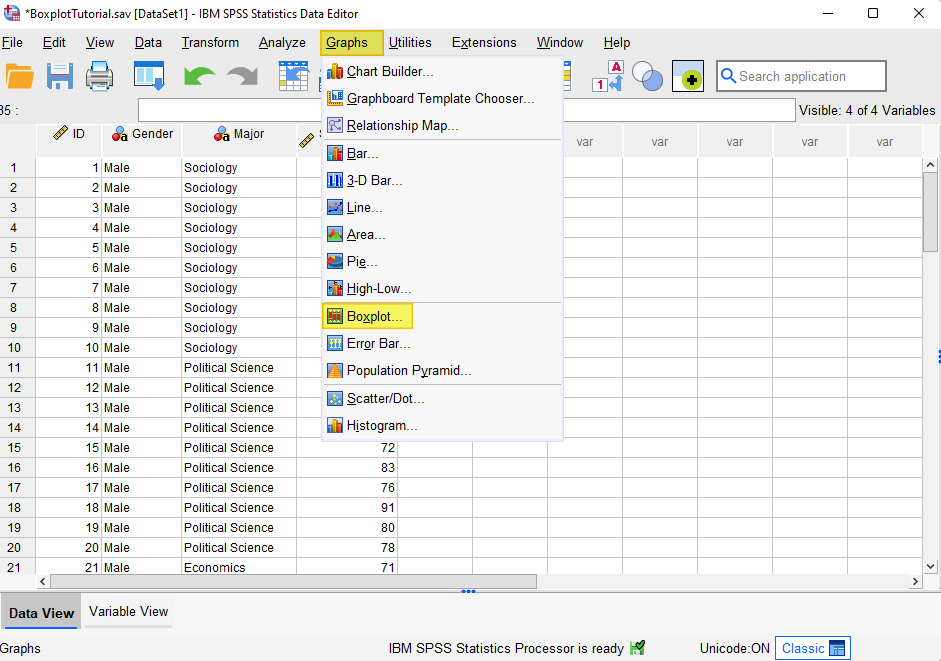
This brings up the following “Boxplot” dialog box:
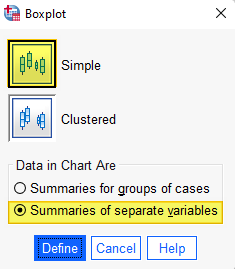
Select the Simple boxplot. Under “Data in Chart Are,” select Summaries of separate variables.
Click Define.
This brings up the “Define Simple Boxplot: Summaries of Separate Variables” dialog box illustrated below.
It is a good idea to click the Reset button to clear any previous settings.
Select the variable for which you wish to create a boxplot (“Statistics Final Exam Score” in our example) and use the arrow button to move it to the Boxes Represent box.

Click OK.
The SPSS Output Viewer will pop up with a “Case Processing Summary” and a boxplot for your variable.
Data Values Illustrated on a Boxplot
The boxplot for students’ Statistics final exam scores created in SPSS is below.
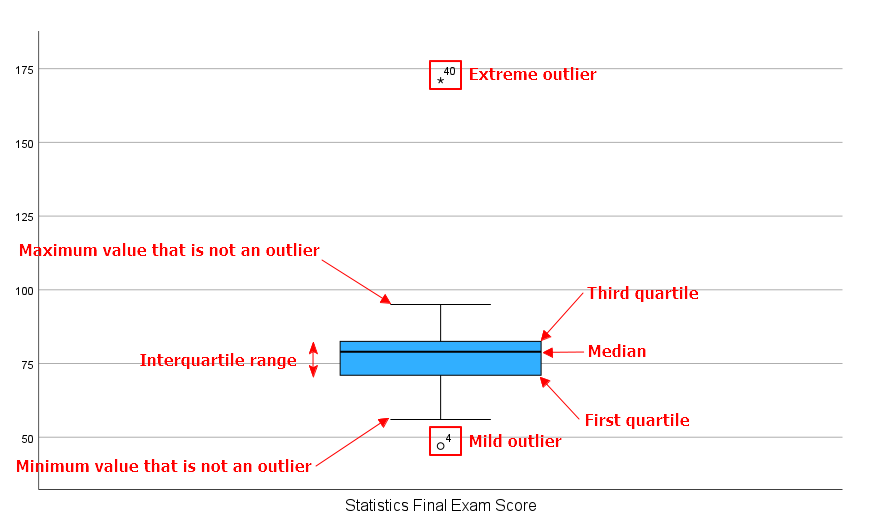
As you can see, boxplots illustrate the following values for a variable:
Five Number Summary
- Minimum value that isn’t an outlier: Represented by the bottom of the vertical line (whisker) that extends from the bottom of the box.
- First Quartile (Q1): The value below which 25% of the values in the data set are found.
- Median: The value that separates the higher half of the data set from the lower half.
- Third Quartile (Q3): The value below which 75% of the values in the data set are found.
- Maximum value that isn’t an outlier: Represented by the top of the vertical line (whisker) that extends from the top of the box.
- Interquartile range (IQR): The box in the boxplot. This is the middle 50% of the data set (between Q1 and Q3).
Outliers
- Mild outliers: Values that are more than 1.5 x IQR below Q1 or above Q3 are represented by circles. SPSS gives us the case numbers for these values. In our data set, case number 4 is a mild outlier.
- Extreme outliers: Values that are more than 3.0 x IQR below Q1 or above Q3 are represented by asterisks. SPSS gives us the case numbers for these values. In our data set, case number 40 is an extreme outlier.
How to Interpret Your Boxplot
Data Distribution and Skewness
Boxplots illustrate whether the distribution of a data set is symmetrical, positively skewed, or negatively skewed.
When the median is in the middle of the box, and the whiskers that extend from each end of the box are approximately equal, the data set is distributed symmetrically.
When the median is closer to the bottom of the box, and the whisker below the box is shorter than the whisker above the box, the data set is positively skewed.
When the median is closer to the top of the box, and whisker above the box is shorter than the whisker below the box, then the data set is negatively skewed. In our example data set, the distribution of students’ Statistics final exam scores is negatively skewed.
Outliers
If your data has outliers, it is a good idea to investigate them. While some outliers are legitimate, others may be the result of errors in our data. Erroneous data values should be corrected if this is possible, and removed if they cannot be corrected.
In our example dataset, case number 4 is a mild outlier. As you can see below, the exam score entered for case number 4 is 47. Without further investigation, we don’t know whether or not this is a legitimate score.
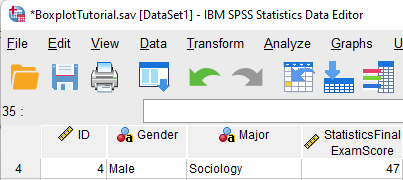
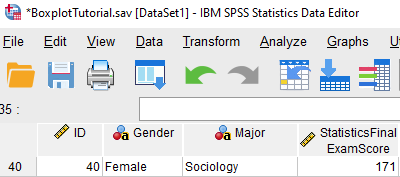
Our example dataset also includes an extreme outlier with a case number of 40. The exam score entered for this case is 171. This value is clearly an error because the maximum exam score possible is 100. As noted above, this score should be corrected or removed from the data set.
Saving Your Boxplot and Adding a Title
We will not save our boxplot because it includes at least one erroneous data value but, if you want to save your boxplot, it is a good idea to give it a title. To do this, double-click on your boxplot in the SPSS Output Viewer to open the Chart Editor.
Click Options-> Title as illustrated below.
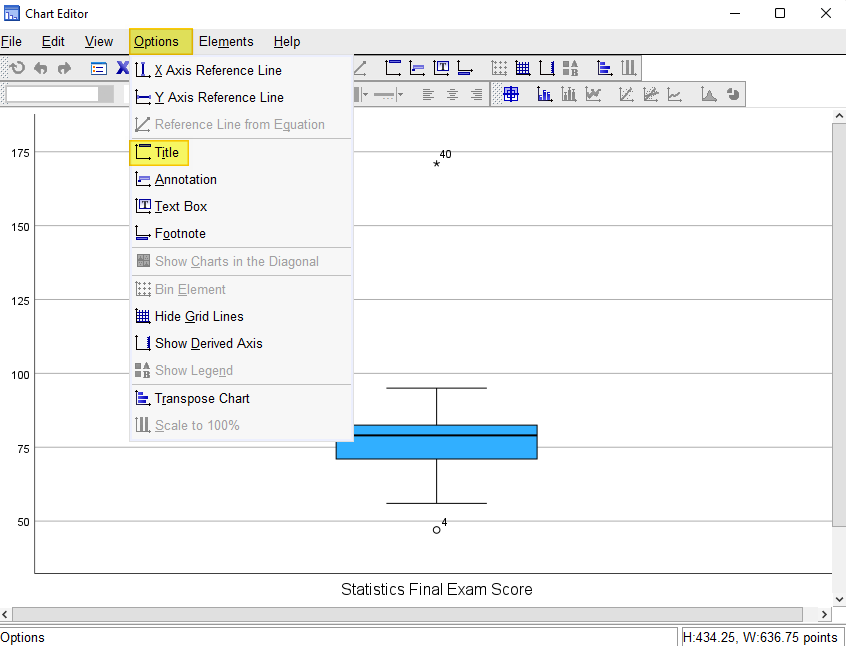
SPSS will add a title bar to your boxplot with the default text “Title.” Overtype this text with the title you want to add. Select the X in the top right corner of the Chart Editor window. Your boxplot will be saved with your title.
You can then right-click on your boxplot within the Output Viewer, and copy it as an image file (which you can then use in other programs). Alternatively, check out our tutorial on exporting SPSS output to other applications such as Word, Excel, or PDF.
***************
That’s it for this quick tutorial. You should now be able to create and interpret a boxplot for a single variable within SPSS. You might also be interested in our tutorial for creating side-by-side boxplots to compare two or more groups.
***************