In this tutorial, we’ll look at how to perform a repeated-measures (or within-subjects) ANOVA in SPSS, and also at how to interpret the result.
A repeated-measures ANOVA design is sometimes used to analyze data from a longitudinal study, where the requirement is to assess the effect of the passage of time on a particular variable. For this tutorial, we’re going to use data from a hypothetical study that looks at whether fear of spiders among arachnophobes increases over time if the disorder goes untreated.
Quick Steps
- Click Analyze -> General Linear Model -> Repeated Measures
- Name your Within-Subject factor, specify the number of levels, then click Add
- Hit Define, and then drag and drop (left to right) a variable for each of the levels you specified (taking care to preserve their correct order)
- Click Options, and tick the Descriptive statistics and Estimate of effect size boxes, and then click Continue
- You’re now ready to run the test. Press the OK button, and your result will pop up in the Output Viewer
The Data
This is the data from our “study” as it appears in the SPSS Data View.
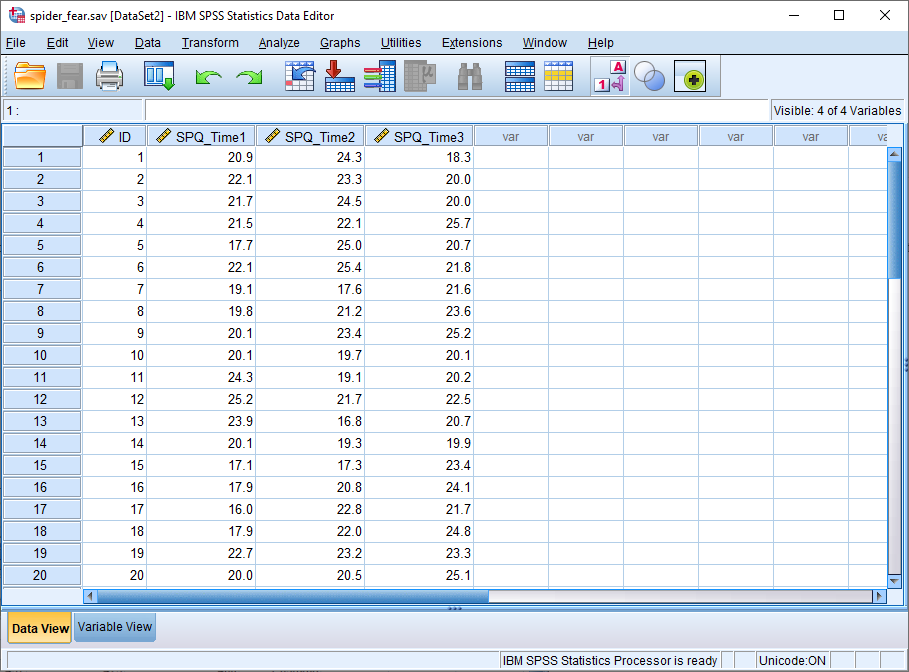
The variable we’re interested in here is SPQ which is a measure of the fear of spiders that runs from 0 to 31. The average score for a person with a spider phobia is 23, which compares to a score of slightly under 3 for a non-phobic.
SPQ is the dependent variable. The independent variable – or, to adopt the terminology of ANOVA, the within-subjects factor – is time, and it has three levels: SPQ_Time1 is the time of the first SPQ assessment; SPQ_Time2 is one year later; and SPQ_Time3 two years later.
The null hypothesis is that the mean SPQ score is the same for all levels of the within-subjects factor. This is what we’ll test with a one-way repeated-measures ANOVA.
Repeated-Measures ANOVA
To start, click Analyze -> General Linear Model -> Repeated Measures. This will bring up the Repeated Measures Define Factor(s) dialog box.
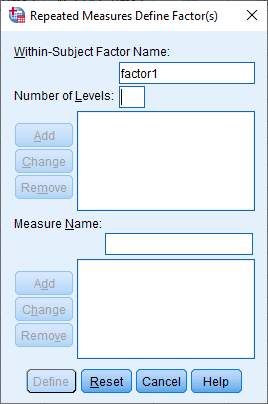
As we noted above, our within-subjects factor is time, so type “time” in the Within-Subject Factor Name box. And we have 3 levels, so input 3 into Number of Levels. Then click Add.
The dialog box should now look like this.
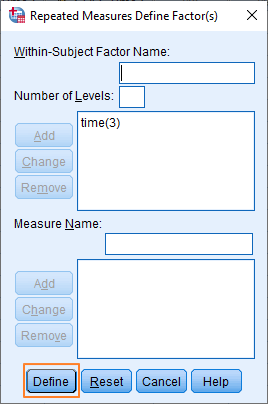
Okay, it’s now time to set up the within-subjects variables (at the moment SPSS knows that our within-subjects factor has three levels, but it doesn’t know which of our variables corresponds to each level). Click on the Define button, which will bring up the Repeated Measures dialog blox.

You’ve got to shift your within-subjects variables over to the Within-Subjects Variables box ensuring you maintain the correct order. You can drag and drop, or use the arrow button in the middle of the box. In our case, it just means moving SPQ_Time1, SPQ_Time2 & SPQ_Time3 into the three slots on the right.
The dialog box should look something like this once you’ve completed this stage.
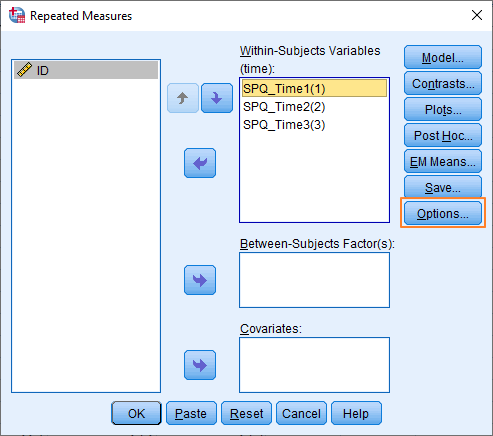
We’re now ready to set up some of the options for the repeated-measures ANOVA. Click on the Options button.
Options
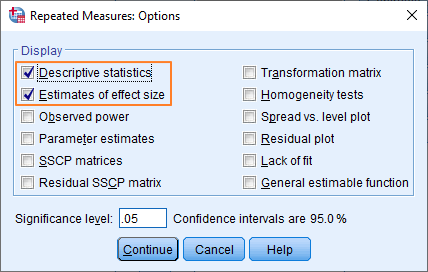
What you see here depends on the version of SPSS you’re using. The most recent version of SPSS (26) has an options dialog box that looks like this.
Previous versions include an option for specifying estimated marginal means. It looks like this.
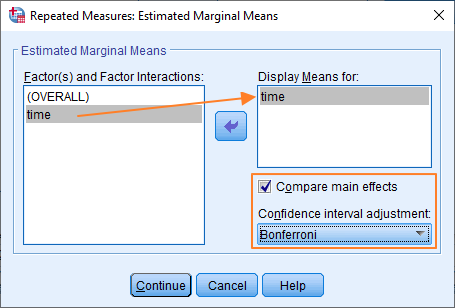
We’re going to assume that you’re using a previous version of SPSS, and you’re seeing the estimated marginal means option. If you’re not, then you need to click on the EM Means button (in the Repeated Measures dialog box) after you’ve finished with the Options dialog box, and set up the estimated marginal means there.
It’s not too difficult to get the options sorted out. You want to display descriptive statistics and estimates of effect size, so tick these options in the Display section (as above). And then in the Estimated Marginal Means section (or dialog box if you’re using the current version of SPSS), move “time” over to the Display Means for box, and then tick Compare main effects, and choose Bonferroni as the Confidence interval adjustment option.
Hit the Continue button(s) once you’ve got this set up.
That’s it, you’re ready to run the test. You should be looking at the original Repeated Measures dialog box. All you’ve got to do is hit OK, and you’ll see the result pop up in the Output Viewer.
The Result
SPSS produces a lot of output for the one-way repeated-measures ANOVA test. For the purposes of this tutorial, we’re going to concentrate on a fairly simple interpretation of all this output. (In future tutorials, we’ll look at some of the more complex options available to you, including multivariate tests and polynomial contrasts).
Descriptive Statistics
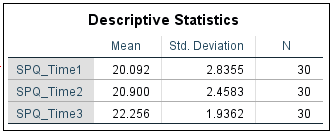
The descriptive statistics that SPSS outputs are easy enough to understand. The comparison between means (see above) gives us an idea of the direction of any possible effect. In our example, it seems as if fear of spiders increases over time, with the greatest increase (20.90 to 22.26 on the SPQ scale) occurring between year 1 (SPQ_Time2) and year 2 (SPQ_Time3). Of course, we won’t know whether these differences in the means reach significance until we look at the result of the ANOVA test.
Assumption of Sphericity
A requirement that must be met before you can trust the p-value generated by the standard repeated-measures ANOVA is the homogeneity-of-variance-of-differences (or sphericity) assumption. For our purposes, it doesn’t matter too much what this means, we just need to know how to figure out whether the requirement has been satisfied.
SPSS tests this assumption by running Mauchly’s test of sphericity.

What we’re looking for here is a p-value that’s greater than .05. Our p-value is .494, which means we meet the assumption of sphericity.
You’ve got to be careful here. This assumption is frequently violated. If it is, in order to calculate a reliable value for p, you’ll need to adjust the degrees of freedom of F in line with the extent to which the assumption is violated. Happily SPSS does this work for you. All you’ve got to do is choose an alternative univariate test. Let’s look at this now.
Tests of Within-Subjects Effects
This is where we read off the result of the repeated-measures ANOVA test.
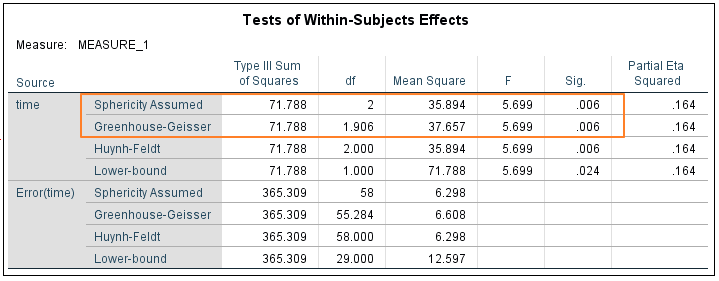
As we have just discussed, our data meets the assumption of sphericity, which means we can read our result straight from the top row (Sphericity Assumed). The value of F is 5.699, which reaches significance with a p-value of .006 (which is less than the .05 alpha level). This means there is a statistically significant difference between the means of the different levels of the within-subjects variable (time).
If our data had not met the assumption of sphericity, we would need to use one of the alternative univariate tests. You’ll notice that these produce the same value for F, but that there is some variation in the reported degrees of freedom. In our case, there is not enough difference to alter the p-value – Greenhouse-Geisser and Huynh-Feldt, both produce significant results (p = .006).
Pairwise Comparisons
Although we know that the differences between the means of our three within-subjects levels are large enough to reach significance, we don’t yet know between which of the various pairs of means the difference is significant. This is where pairwise comparisons come into play.
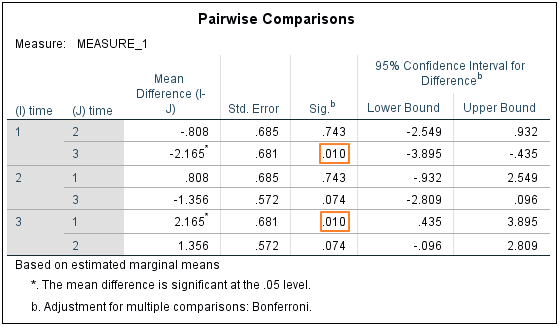
This table features three unique comparisons between the means for SPQ_Time1, SPQ_Time2 and SPQ_Time3. Only one of the differences reaches significance, and that’s the difference between the means for SPQ_Time1 and SPQ_Time 3 (see above). It is worth noting that SPSS is using an adjusted p-value here in order to control for multiple comparisons, and that the program lets you know if a mean difference has reached significance by attaching an asterisk to the value in column 3.
Report the Result
When reporting the result it’s normal to reference both the ANOVA test and any post hoc analysis that has been done.
Thus, given our example, you could write something like:
A repeated-measures ANOVA determined that mean SPQ scores differed significantly across three time points (F(2, 58) = 5.699, p = .006). A post hoc pairwise comparison using the Bonferroni correction showed an increased SPQ score between the initial assessment and follow-up assessment one year later (20.1 vs 20.9, respectively), but this was not statistically significant (p = .743). However, the increase in SPQ score did reach significance when comparing the initial assessment to a second follow-up assessment taken two years after the original assessment (20.1 vs 22.26, p = .010). Therefore, we can conclude that the results for the ANOVA indicate a significant time effect for untreated fear of spiders as measured on the SPQ scale.
Alternatively, check out our tutorial on reporting a repeated-measures ANOVA from SPSS in APA style.
***************
Okay, that’s all for this tutorial. You should now be able to run a repeated-measures ANOVA, test the assumption of sphericity, make use of a pairwise comparison, and report the result. Check out our tutorial if you’d like to export the SPSS output for your ANOVA to another application such as Word, Excel, or PDF.